常见算法思想的分析

算法思想是解决问题的核心，万丈高楼起于平地，在算法中也是如此，本章主要学习 6 中常见的算法分别为：递归算法、分治算法、贪心算法、回溯算法、动态规划、枚举算法，95% 的算法都是基于这 6 种算法思想，接下来介绍一下这 6 种算法思想，帮助我们理解及解决各种算法问题。

递归算法

算法策略

递归算法是一种直接或者间接调用自身函数或者方法的算法。

递归算法的实质是把问题分解成规模缩小的同类问题的子问题，然后递归调用方法来表示问题的解。递归算法对解决一大类问题很有效，它可以使算法简洁和易于理解。

优缺点：

• 优点
  • 实现简单易上手。
• 缺点
  • 递归算法对常用的算法如普通循环等，运行效率较低；
  • 在递归调用的过程当中系统为每一层的返回点、局部量等开辟了栈来存储，递归太深，容易发生栈溢出。

适用场景

递归算法一般用于解决三类问题：

• 数据的定义是按递归定义的。（斐波那契数列）
• 问题解法按递归算法实现。（回溯）
• 数据的结构形式是按递归定义的。（树的遍历，图的搜索）

递归的解题策略：

• 第一步：明确你这个函数的输入输出，先不管函数里面的代码什么，而是要先明白，你这个函数的输入是什么，输出是什么，功能是什么，要完成什么样的一件事。
• 第二步：寻找递归结束条件，我们需要找出什么时候递归结束，之后直接把结果返回。
• 第三步：明确递归关系式，怎么通过各种递归调用来组合解决当前问题。

使用递归算法求解的一些经典问题

• 斐波那契数列
• 汉诺塔问题
• 树的遍历及相关操作

DOM 树为例

下面以以 DOM 为例，实现一个 document.getElementById 功能

由于 DOM 是一棵树，而树的定义本身就是用的递归定义，所以用递归的方法处理树，会非常地简单自然。

第一步：明确你这个函数的输入输出

从 DOM 根节点一层层往下递归，判断当前节点的 id 是否是我们要寻找的 id='d-cal'

输入：DOM 根节点 document ，我们要寻找的 id='d-cal'

输出：返回满足 id='sisteran' 的子结点

function getElementById(node, id) {}

第二步：寻找递归结束条件

从 document 开始往下找，对所有子结点递归查找他们的子结点，一层一层地往下查找：

• 如果当前结点的 id 符合查找条件，则返回当前结点
• 如果已经到了叶子结点了还没有找到，则返回 null

function getElementById(node, id) {
  // 当前结点不存在，已经到了叶子结点了还没有找到，返回 null
  if (!node) return null
  // 当前结点的 id 符合查找条件，返回当前结点
  if (node.id === id) return node
}

第三步：明确递归关系式

当前结点的 id 不符合查找条件，递归查找它的每一个子结点

function getElementById(node, id) {
  // 当前结点不存在，已经到了叶子结点了还没有找到，返回 null
  if (!node) return null
  // 当前结点的 id 符合查找条件，返回当前结点
  if (node.id === id) return node
  // 前结点的 id 不符合查找条件，继续查找它的每一个子结点
  for (var i = 0; i < node.childNodes.length; i++) {
    // 递归查找它的每一个子结点
    var found = getElementById(node.childNodes[i], id)
    if (found) return found
  }
  return null
}

就这样，我们的一个 document.getElementById 功能已经实现了,

最后在控制台验证一下，执行结果如下图所示：

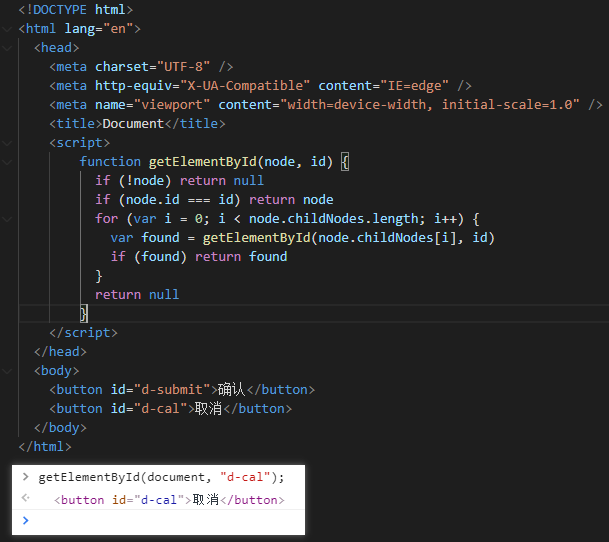
使用递归的优点是代码简单易懂，缺点是效率比不上非递归的实现。Chrome 浏览器的查 DOM 是使用非递归实现。非递归要怎么实现呢？

如下代码：

function getByElementId(node, id) {
  //遍历所有的Node
  while (node) {
    if (node.id === id) return node
    node = nextElement(node)
  }
  return null
}

还是依次遍历所有的 DOM 结点，只是这一次改成一个 while 循环，函数 nextElement 负责找到下一个结点。所以关键在于这个 nextElement 如何实现非递归查找结点功能：

// 深度遍历
function nextElement(node) {
  // 先判断是否有子结点
  if (node.children.length) {
    // 有则返回第一个子结点
    return node.children[0]
  }
  // 再判断是否有相邻结点
  if (node.nextElementSibling) {
    // 有则返回它的下一个相邻结点
    return node.nextElementSibling
  }
  // 否则，往上返回它的父结点的下一个相邻元素，相当于上面递归实现里面的for循环的i加1
  while (node.parentNode) {
    if (node.parentNode.nextElementSibling) {
      return node.parentNode.nextElementSibling
    }
    node = node.parentNode
  }
  return null
}

在控制台里面运行这段代码，同样也可以正确地输出结果。不管是非递归还是递归，它们都是深度优先遍历，这个过程如下图所示:

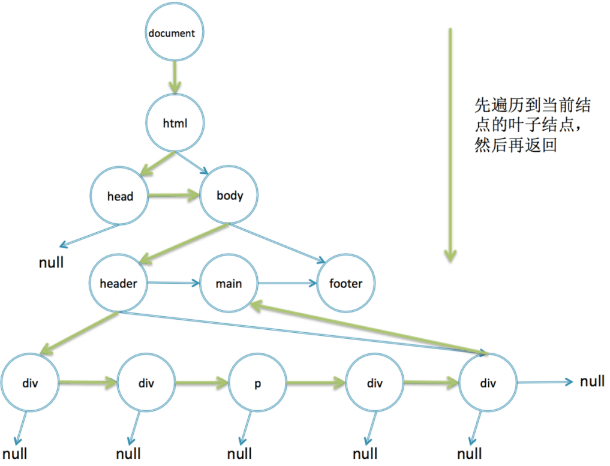
实际上 getElementById 浏览器是用的一个哈希 map 存储的，根据 id 直接映射到 DOM 结点，而 getElementsByClassName 就是用的这样的非递归查找。

具体详见：我接触过的前端数据结构与算法

分治算法

算法策略

在计算机科学中，分治算法是一个很重要的算法，快速排序、归并排序等都是基于分治策略进行实现的，所以，建议理解掌握它。

分治，顾名思义，就是分而治之，将一个复杂的问题，分成两个或多个相似的子问题，在把子问题分成更小的子问题，直到更小的子问题可以简单求解，求解子问题，则原问题的解则为各子问题解的合并。

适用场景

当出现满足以下条件的问题，可以尝试只用分治策略进行求解：

• 原始问题可以分成多个相似的子问题
• 子问题可以很简单的求解
• 原始问题的解是子问题解的合并
• 各个子问题是相互独立的，不包含相同的子问题

分治的解题策略：

• 第一步：分解，将原问题分解为若干个规模较小，相互独立，与原问题形式相同的子问题
• 第二步：解决，解决各个子问题
• 第三步：合并，将各个子问题的解合并为原问题的解

使用分治法求解的一些经典问题

• 二分查找
• 归并排序
• 快速排序
• 汉诺塔问题
• React 时间分片

二分查找

也称折半查找算法，它是一种简单易懂的快速查找算法。例如我随机写 0-100 之间的一个数字，让你猜我写的是什么？你每猜一次，我就会告诉你猜的大了还是小了，直到猜中为止。

第一步：分解

每次猜的数都把上一次的结果分出大的一组和小的一组，两组相互独立

• 选择数组中的中间数

function binarySearch(items, item) {
  // low、mid、high将数组分成两组
  var low = 0,
    high = items.length - 1,
    mid = Math.floor((low + high) / 2),
    elem = items[mid]
  // ...
}

第二步：解决子问题

查找数与中间数对比

• 比中间数低，则去中间数左边的子数组中寻找；
• 比中间数高，则去中间数右边的子数组中寻找；
• 相等则返回查找成功

while (low <= high) {
  // 比中间数高
  if (elem < item) {
    low = mid + 1
  } else if (elem > item) {
    // 比中间数低
    high = mid - 1
  } else {
    // 相等
    return mid
  }
}

第三步：合并

function binarySearch(items, item) {
  var low = 0,
    high = items.length - 1,
    mid,
    elem
  while (low <= high) {
    mid = Math.floor((low + high) / 2)
    elem = items[mid]
    if (elem < item) {
      low = mid + 1
    } else if (elem > item) {
      high = mid - 1
    } else {
      return mid
    }
  }
  return -1
}

需要注意的是：二分法只能应用于数组有序的情况，如果数组无序，二分查找就不能起作用了

function binarySearch(items, item) {
  // 快排
  quickSort(items)
  var low = 0,
    high = items.length - 1,
    mid,
    elem
  while (low <= high) {
    mid = Math.floor((low + high) / 2)
    elem = items[mid]
    if (elem < item) {
      low = mid + 1
    } else if (elem > item) {
      high = mid - 1
    } else {
      return mid
    }
  }
  return -1
}

// 测试
var arr = [2, 3, 1, 4]
binarySearch(arr, 3)
// 2

binarySearch(arr, 5)
// -1

贪心算法

算法策略

贪心算法，故名思义，总是做出当前的最优选择，即期望通过局部的最优选择获得整体的最优选择。

某种意义上说，贪心算法是很贪婪、很目光短浅的，它不从整体考虑，仅仅只关注当前的最大利益，所以说它做出的选择仅仅是某种意义上的局部最优，但是贪心算法在很多问题上还是能够拿到最优解或较优解，所以它的存在还是有意义的。

适用场景

在日常生活中，我们使用到贪心算法的时候还是挺多的，例如：

从 100 章面值不等的钞票中，抽出 10 张，怎样才能获得最多的价值？

我们只需要每次都选择剩下的钞票中最大的面值，最后一定拿到的就是最优解，这就是使用的贪心算法，并且最后得到了整体最优解。

但是，我们任然需要明确的是，期望通过局部的最优选择获得整体的最优选择，仅仅是期望而已，也可能最终得到的结果并不一定不能是整体最优解。

例如：求取 A 到 G 最短路径：

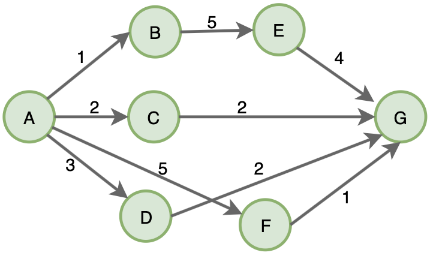
根据贪心算法总是选择当前最优选择，所以它首先选择的路径是 AB，然后 BE、EG，所得到的路径总长为 1 + 5 + 4 = 10，然而这并不是最短路径，最短路径为 A->C->G : 2 + 2 = 4，所以说，贪心算法得到得并不一定是最优解。

那么一般在什么时候可以尝试选择使用贪心算法呢？

当满足一下条件时，可以使用：

• 原问题复杂度过高
• 求全局最优解的数学模型难以建立或计算量过大
• 没有太大必要一定要求出全局最优解，“比较优”就可以

如果使用贪心算法求最优解，可以按照以下 步骤求解 ：

• 首先，我们需要明确什么是最优解（期望）
• 然后，把问题分成多个步骤，每一步都需要满足：
  • 可行性：每一步都满足问题的约束
  • 局部最优：每一步都做出一个局部最优的选择
• 不可取消：选择一旦做出，在后面遇到任何情况都不可取消
• 最后，叠加所有步骤的最优解，就是全局最优解

经典案例：活动选择问题

使用贪心算法求解的经典问题有：

• 最小生成树算法
• 单源最短路径的 迪杰斯特拉算法（Dijkstra 算法）
• 哈夫曼编码（Huffman 压缩编码）
• 背包问题
• 活动选择问题等
  其中活动选择问题是最简单的，这里详细介绍这个。

活动选择问题是《算法导论》上的例子，也是一个非常经典的问题。有 n 个活动（a1,a2,…,an）需要使用同一个资源（例如教室），资源在某个时刻只能供一个活动使用。每个活动 ai 都有一个开始时间 si 和结束时间 fi 。一旦被选择后，活动 ai 就占据半开时间区间 [si,fi) 。如果 [si,fi) 和 [sj,fj) 互不重叠，ai 和 aj 两个活动就可以被安排在这一天。

该问题就是要安排这些活动，使得尽量多的活动能不冲突的举行。例如下图所示的活动集合 S，其中各项活动按照结束时间单调递增排序。

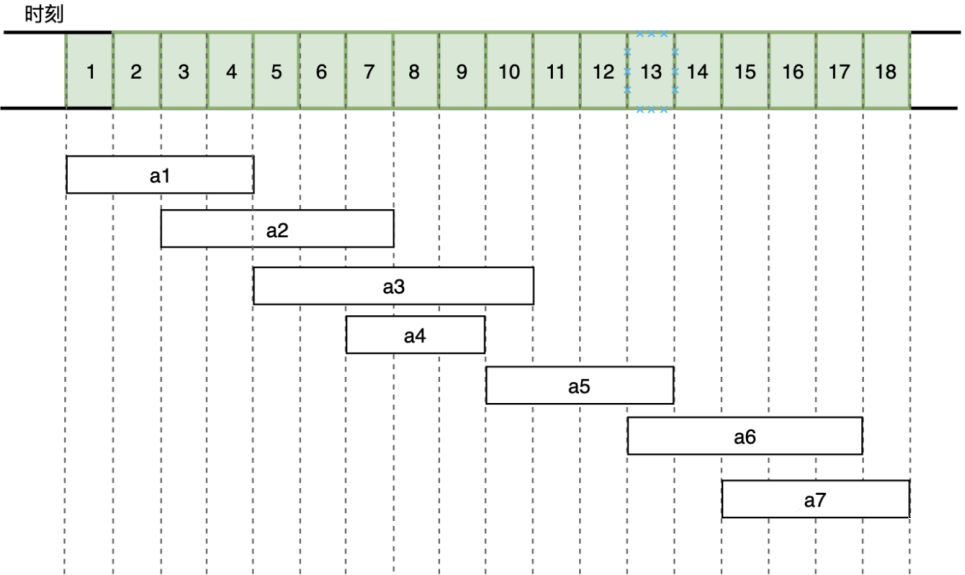
共有 7 个活动，它们在 18 个小时内需要占用的时间如上图，如何选择活动，能让这间教室利用率最高喃（能够举行更多的活动）？

贪心算法对这种问题的解决很简单的，它开始时刻开始选择，每次选择开始时间与与已选择活动不冲突的，结束时间又比较靠前的活动，这样会让剩下的时间区间更长。

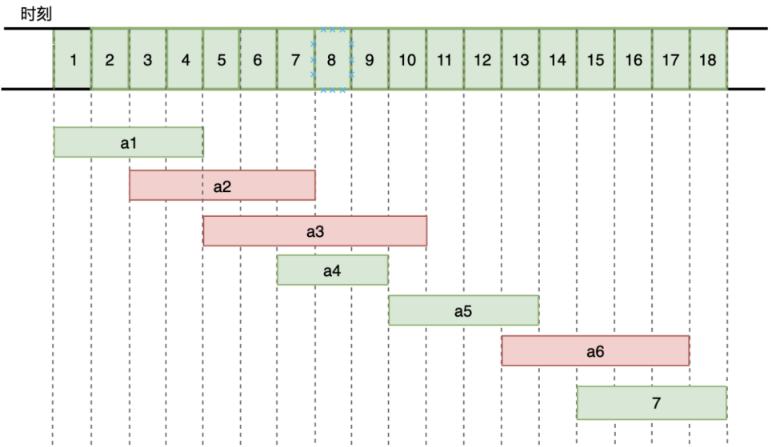
• 首先 a1 活动的结束时间最早，选择 a1 活动
• a1 结束后，a2 有时间冲突不可选择，a3、a4 都可选择，但 a4 结束时间最早，选择 a4
• 依次选择时间没有冲突的，又结束时间最早的活动
  最终选择活动为 a1，a4，a5，a7。为最优解。

回溯算法

算法策略

回溯算法是一种搜索法，试探法，它会在每一步做出选择，一旦发现这个选择无法得到期望结果，就回溯回去，重新做出选择。深度优先搜索利用的就是回溯算法思想。

适用场景

回溯算法很简单，它就是不断的尝试，直到拿到解。它的这种算法思想，使它通常用于解决广度的搜索问题，即从一组可能的解中，选择一个满足要求的解。

使用回溯算法的经典案例

• 深度优先搜索
• 0-1 背包问题
• 正则表达式匹配
• 八皇后
• 数独
• 全排列
  这里以正则表达式匹配为例，介绍一下

正则表达式匹配

var string = 'abbc'
var regex = /ab{1,3}c/
console.log(string.match(regex))
// ["abbc", index: 0, input: "abbc", groups: undefined]

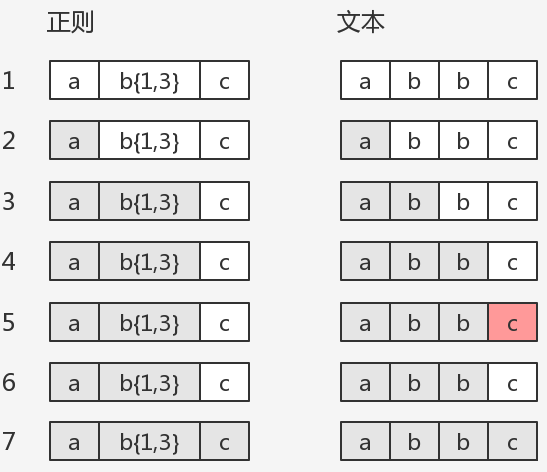
在第 5 步匹配失败，此时 b{1,3} 已经匹配到了两个 b 正在尝试第三个 b ，结果发现接下来是 c 。此时就需要回溯到上一步， b{1,3} 匹配完毕（匹配到了 bb ），然后再匹配 c ，匹配到了 c 匹配结束。

动态规划

算法策略

动态规划也是将复杂问题分解成小问题求解的策略，与分治算法不同的是，分治算法要求各子问题是相互独立的，而动态规划各子问题是相互关联的。

所以，动态规划适用于子问题重叠的情况，即不同的子问题具有公共的子子问题，在这种情况下，分治策略会做出很多不必要的工作，它会反复求解那些公共子子问题，而动态规划会对每个子子问题求解一次，然后保存在表格中，如果遇到一致的问题，从表格中获取既可，所以它无需求解每一个子子问题，避免了大量的不必要操作。

适用场景

动态规划适用于求解最优解问题，比如，从面额不定的 100 个硬币中任意选取多个凑成 10 元，求怎样选取硬币才可以使最后选取的硬币数最少又刚好凑够了 10 元。这就是一个典型的动态规划问题。它可以分成一个个子问题（每次选取硬币），每个子问题又有公共的子子问题（选取硬币），子问题之间相互关联（已选取的硬币总金额不能超过 10 元），边界条件就是最终选取的硬币总金额为 10 元。

针对上例，也许你也可以说，我们可以使用回溯算法，不断的去试探，但回溯算法是使用与求解广度的解（满足要求的解），如果是用回溯算法，我们需要尝试去找所有满足条件的解，然后找到最优解，时间复杂度为 O(2^n^) ，这性能是相当差的。大多数适用于动态规划的问题，都可以使用回溯算法，只是使用回溯算法的时间复杂度比较高而已。

最后，总结一下，我们使用动态规划求解问题时，需要遵循以下几个重要步骤：

• 定义子问题
• 实现需要反复执行解决的子问题部分
• 识别并求解出边界条件

使用动态规划求解的一些经典问题

爬楼梯问题：假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？
背包问题：给出一些资源（有总量及价值），给一个背包（有总容量），往背包里装资源，目标是在背包不超过总容量的情况下，装入更多的价值
硬币找零：给出面额不定的一定数量的零钱，以及需要找零的钱数，找出有多少种找零方案
图的全源最短路径：一个图中包含 u、v 顶点，找出从顶点 u 到顶点 v 的最短路径
最长公共子序列：找出一组序列的最长公共子序列（可由另一序列删除元素但不改变剩下元素的顺序实现）
这里以最长公共子序列为例。

爬楼梯问题

这里以动态规划经典问题爬楼梯问题为例，介绍求解动态规划问题的步骤。

第一步：定义子问题

如果用 dp[n] 表示第 n 级台阶的方案数，并且由题目知：最后一步可能迈 2 个台阶，也可迈 1 个台阶，即第 n 级台阶的方案数等于第 n-1 级台阶的方案数加上第 n-2 级台阶的方案数

第二步：实现需要反复执行解决的子子问题部分

dp[n] = dp[n−1] + dp[n−2]

第三步：识别并求解出边界条件

// 第 0 级 1 种方案
dp[0] = 1
// 第 1 级也是 1 种方案
dp[1] = 1

最后一步：把尾码翻译成代码，处理一些边界情况

let climbStairs = function (n) {
  let dp = [1, 1]
  for (let i = 2; i <= n; i++) {
    dp[i] = dp[i - 1] + dp[i - 2]
  }
  return dp[n]
}

复杂度分析：

• 时间复杂度：O(n)
• 空间复杂度：O(n)

优化空间复杂度：

let climbStairs = function (n) {
  let res = 1,
    n1 = 1,
    n2 = 1
  for (let i = 2; i <= n; i++) {
    res = n1 + n2
    n1 = n2
    n2 = res
  }
  return res
}

空间复杂度：O(1)

枚举算法

枚举算法本质上就是搜索算法

算法策略

枚举算法的思想是：将问题的所有可能的答案一一列举，然后根据条件判断此答案是否合适，保留合适的，丢弃不合适的。

优缺点：

• 优点：算法简单，在局部地方使用枚举法，效果十分的好
• 缺点：运算量过大，当问题的规模变大的时候，循环的阶数越大，执行速度越慢

解题思路

确定枚举对象、枚举范围和判定条件。
逐一列举可能的解，验证每个解是否是问题的解。

枚举算法步骤：

• 确定解题的可能范围，不能遗漏任何一个真正解，同时避免重复。
• 判定是否是真正解的方法。
• 为了提高解决问题的效率，使可能解的范围将至最小

枚举算法的流程图如下所示：

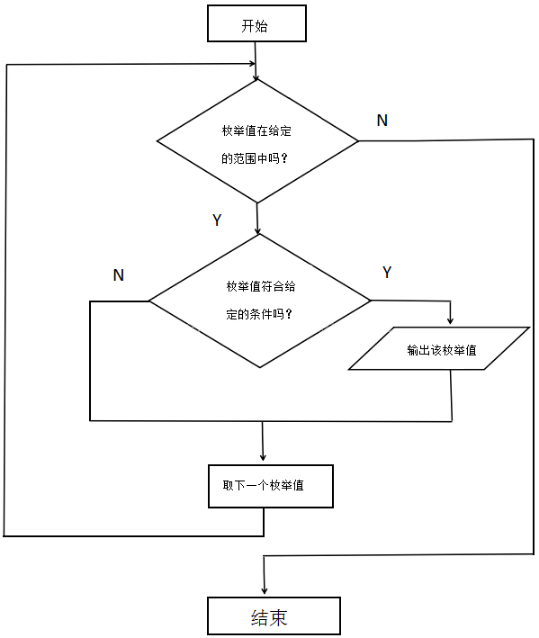
百钱买百鸡问题

有一个人有一百块钱，打算买一百只鸡。到市场一看，公鸡一只 3 元,母鸡一只 5 元,小鸡 3 只 1 元,试求用 100 元买 100 只鸡,各为多少才合适?

根据题意我们可以得到方程组：

// x 公鸡，y 母鸡 z 小鸡
3X + 5Y + Z/3 = 100
X + Y + Z = 100
(100 > X,Y,Z > 0, Z%3 == 0)

根据这两个公式，我们可以写出最为简单的代码，一一列举所有解进行枚举

let x, y, z
for (x = 0; x < 100; x++) {
  for (y = 0; y < 100; y++) {
    for (z = 0; z < 100; ) {
      if (x + y + z == 100 && 3 * x + 5 * y + z / 3 == 100) {
        console.log(`公鸡：${x}只，母鸡：${y}只，小鸡：${z}只`)
      }
      z += 3
    }
  }
}

然而我们可以根据已知条件来进行优化代码，减少枚举的次数：

三种鸡的和是固定的，我们只要枚举二种鸡（x,y），第三种鸡就可以根据约束条件求得z = 100 - x - y，这样就缩小了枚举范围。
另外我们根据方程特点，可以消去一个未知数，得到下面

4X + 7Y = 100
X + Y + Z = 100
(X,Y,Z > 0, Z%3 == 0) =>> 0 <= x < = 25

因此代码可以优化为下面这样子：

for (x = 0; x <= 25; x++) {
  y = 100 - 4 * x
  if (y % 7 == 0 && y >= 0) {
    y /= 7
    z = 100 - x - y
    if (z % 3 == 0 && 3 * x + 5 * y + z / 3 == 100) {
      console.log(`公鸡：${x}只，母鸡：${y}只，小鸡：${z}只`)
    }
  }
}

运行结果如下:

公鸡：4 只，母鸡：12 只，小鸡：84 只
公鸡：11 只，母鸡：8 只，小鸡：81 只
公鸡：18 只，母鸡：4 只，小鸡：78 只
公鸡：25 只，母鸡：0 只，小鸡：75 只

采用枚举的方法进行问题求解，需要注意 3 个问题：

• 简单数学模型，数学模型中变量数量尽量少，它们之间相互独立。这样问题解的搜索空间的维度就小，反应到程序代码中，循环嵌套的层次就会少。我们上面从 3 维优化到一维。
• 减少搜索的空间。利用已有知识，缩小数学模型中各个变量的取值范围，避免不必要的计算。反应到程序代码中，循环体被执行的次数少
• 采用合适的搜索顺序。对搜索空间的遍历顺序要与数学模型中的条件表达式一致。